Peak power from maximal vertical jump height determines radial bone strength better than hand grip strength in healthy individuals
Last Updated: 2021-03-06
Affiliations
1 - Department of Kinesiology, California State University, East Bay, Hayward, CA
Corresponding Author:
Vanessa R Yingling, PhD FACSM
Department of Kinesiology,
California State University, East Bay,
25800 Carlos Bee Boulevard,
Hayward, CA 94542.
Twitter: YinglingV
Email: vanessa.yingling@csueastbay.edu
Abstract
Osteoporosis is considered a pediatric disease with geriatric consequences. However, measuring bone strength in children is complex and creates a practical problem for health professionals, teachers and parents. Based on the muscle-bone relationship, a potential avenue for monitoring bone health is muscle fitness testing. A non-invasive measure of muscle fitness that correlates to bone strength may provide a means to monitor bone strength throughout the lifespan. Therefore, the purpose of this study was to investigate the relationship between common muscle fitness tests, grip strength and peak power (PP) calculated from maximal vertical jump height,and bone strength in the radial diaphysis and epiphysis of a healthy adult population. Healthy participants (n=147 (81 female)) performed a bilateral grip strength test using a hand dynamometer, and a maximal vertical jump test. PP was calculated from maximal jump height using the Sayer’s equation. Bone strength parameters, Moment of inertia (MoI), cortical area (CoA), cortical bone mineral density (cBMD), and polar strength-strain index (SSIp) were measured at the 66% radial site (cortical bone site) using peripheral Quantitative Computed Tomography (pQCT). At the 4% (trabecular bone) site, volumetric bone mineral content (vBMC.tb), volumetric bone mineral density (vBMD.tb), total area (ToA.tb) and bone strength index-compression (BSIc) were measured. Hierarchical multiple regression analyses determined the relationship of each muscle function test for each bone envelope (cortical and trabecular). For the cortical bone measurements, RGS, CGS and PP were all significantly associated with CoA, MoI, and SSIp. PP explained a greater percent of the variance for bone strength parameters (SSIp) compared to RGS, but not to CGS. For the trabecular bone envelope, PP explained a greater percent of the variance for bone strength parameters (BSIc) to a greater extent compared to both CGS and RGS. PP was a significant predictor variable of bone strength at both trabecular and cortical radial sites. Interestingly PP, a lower limb measurement, explained the most variance in the bone strength of the upper limb.
Introduction
Osteoporotic fractures create a large burden on society in terms of cost, morbidity and mortality. In fact, hip fractures, estimated at an incidence of 1.7 million annually in 1990, are expected to reach 6.3 million per year globally by 2050 (Cooper, Campion, & Melton, 1992; Marks, 2009). Optimizing bone strength during development is one strategy to prevent fractures later in life (K. Janz, 2002). Osteoporosis is commonly termed “a pediatric condition with geriatric consequences” (Golden, 2000). Higher bone density and increased bone size have been identified in athletes compared to sedentary controls, illustrating the positive effect of physical activity on bone (Greene, Naughton, Bradshaw, Moresi, & Ducher, 2012; Haapasalo et al., 2000). Increased muscle and cortical bone strength in the racket and throwing arm of racket sport athletes and baseball pitchers have been reported (Haapasalo et al., 2000; Kannus et al., 1995; S. J. Warden et al., 2014; Warden et al., 2019). In addition, athletes who started their sport prior to puberty had greater increases in cortical bone strength compared to athletes who started training after puberty (Kannus et al., 1995). The distal radius, a primary site of osteoporotic fracture (Földhazy, Arndt, Milgrom, Finestone, & Ekenman, 2005; Nellans, Kowalski, & Chung, 2012), is comprised of predominantly trabecular bone. Preliminary results reported benefits of exercise on trabecular bone envelopes in young women with low bone mass (Lambert, Beck, Harding, Watson, & Weeks, 2019). Trabecular bone thickness was also positively correlated to both years of running and weekly running distance, and negatively correlated with age at onset of running (Best, Holt, Troy, & Hamill, 2017). Exercise, especially in young people may have benefits to both cortical and trabecular bone strength parameters.
The current clinical diagnostic tool for osteoporosis is dual x-ray absorptiometry (DXA) scanning, but it is primarily used on older women. There are no testing recommendations for monitoring bone health for prevention and screening purposes in healthy adults or youth. Monitoring bone strength is challenging. Measuring bone strength is complex and requires measurements of bone size and shape (architecture) as well as material properties, such as mineral density (Van der Meulen, Jepsen, & Mikić, 2001). DXA determines bone strength by areal bone mineral density (aBMD), a measurement that does not quantify the 3-D aspects of bone architecture. Bone strength analysis via peripheral quantitative computed tomography (pQCT) has advantages over DXA since it quantifies bone size, 3-D architecture and cortical bone mineral density (cBMD). The polar strength-strain index (SSIp), an output from the pQCT analysis, provides a good in-vivo approximation for bone strength (Augat, Iida, Jiang, Diao, & Genant, 1998; Ferretti, Cointry, Capozza, Capiglioni, & Chiappe, 2001). Although pQCT captures the architectural parameters of a person’s bone, similar to DXA, the complexity and availability of these devices creates a practical problem for clinicians, coaches and teachers for monitoring bone health development in healthy adults and youth.
Based on the muscle-bone relationship, a potential avenue for monitoring bone health is muscle fitness testing. Multiple studies have correlated muscle cross-sectional area with bone strength in the upper limb (Lorbergs, Farthing, Baxter-Jones, & Kontulainen, 2011; Sumnik et al., 2006) lower limb (Macdonald, Kontulainen, Petit, Janssen, & McKay, 2006) and whole body (Schoenau, Neu, Beck, Manz, & Rauch, 2002). Muscle cross- sectional area has often been used as a surrogate for muscle strength by investigators and clinicians. However, measurement of muscle cross-sectional area and the parameters contributing to muscle force including measures of architecture and fiber length require invasive and/or expensive clinical imaging techniques, once again limiting the use of these measurements for clinicians, coaches and health and fitness professionals.
Therefore, muscular fitness measures may serve as a better proxy than muscle cross-sectional area to assess the effects of bone-enhancing physical activity on bone strength, similar to aerobic fitness measures representing the cumulative effects of cardiovascular physical activity (K. F. Janz, Letuchy, Burns, Francis, & Levy, 2015). However, comparisons of muscle fitness tests to bone strength in specific bones (lower vs. upper) and bone types (cortical vs. trabecular) in healthy populations is lacking in the literature. Therefore, the purpose of the current study was to determine if grip strength (absolute and relative) was a better predictor variable of radial strength (cortical and trabecular regions) compared to peak power (PP) calculated from maximal vertical jump height. We hypothesized that 1) PP calculated from a maximal vertical jump determines radial bone strength similar to grip strength and 2) PP calculated from a maximal vertical jump determines both trabecular and cortical bone strength in the radius.
Methods
Recruitment and Participant Characteristics
Participants for this cross-sectional study were recruited from the population (faculty, staff and students) of a university in the western United States. Recruitment included posted flyers, emails to the university community and word of mouth advertisement. One hundred forty-seven participants (13.3% African American/Black, 17.9% Latina/o, 28.6% White, 27.6 % Asian/Pacific Islander, 1.0 % American Indian or Alaskan Native and 11.7% Mixed Race or Unknown) (n=81 female) were included in the study. Two datasets were combined for these analyses. Methods were similar for both datasets, but one was collected on university athletes and the other on the general healthy university population. A one-way MANOVA was run to determine if athlete status affected the results; it did not (F (2,144) =3.009, p=0.052, Wilk’s λ = 0.960, partial η2=0.04). As a result, the two datasets were merged for the final analyses. Radial scans were used for these analyses and only tibial data of one dataset has been previously published (Yingling, Webb, Inouye, O, & Sherwood, 2017). A general health and demographic survey was completed by all participants. Participants were excluded if they had a history of any diseases that might influence bone health (endocrine diseases, gastrointestinal disorders, and eating disorders), smoked or were pregnant. All participants were informed of the risks and benefits of the study and provided written informed consent. The study was approved by the California State University, East Bay Institutional Review Board (IRB) (CSUEB-IRB-2016-223-F).
Anthropometric Measures
Standing height was measured using a stadiometer (Seca, Chino, CA) to the nearest 0.1 cm. Body mass, lean body mass and body fat percentage were measured using the Bod Pod (BOD POD ® 2007A; Life Measurement Inc, Concord, CA). To obtain an accurate reading, participants were instructed to refrain from exercising and food or drink consumption 3 to 5 hours prior to testing.
Bone Assessment by pQCT
Peripheral quantitative computed tomography (pQCT) (XCT 2000 Stratec Medizintechnik, Pforzheim, Germany) scans were used to assess bone strength measures of the dominant radius. Radial dominance was determined by asking participants, “Which hand do you write with?”. Radial length was measured with elbow extended, from elbow crease to joint line proximal to the carpal bones. The length measurement was repeated twice, and the average was taken. For all participants, a 30 mm planar scout scan was performed to locate the distal end of the radius to determine the 4% and 66% sites of the radial length, after which the two sites were scanned. The voxel size was set to 0.5 mm, slice thickness was 2 mm and the scanning speed was 30 mm/s. Slice images were analyzed using manufacturer’s software (version 6.20). Regions of Interest (ROI) were identified using auto find and minimize functions of the 2000L software package but manual corrections were made using visual check as necessary. The 4% site was predominantly trabecular bone and a contour mode 3, peel mode 4 and a threshold of 169 mg/cm3 were used for the analysis. Bone strength is measured through a combination of the size and geometry (architecture) measurements as well as bone’s material properties (bone mineral density). Trabecular bone outcome measures included measures of bone size, volumetric bone mineral content (vBMC (mg/mm)), and geometry measured by total area (ToA.tb (mm2)) as well as volumetric bone mineral density (vBMD.tb (mg/cm3)). Bone strength for the 4% radial site was Bone Strength Index in compression (BSIc), a combination of both density and architecture (formula below; S. A. Kontulainen et al., 2008).
\[ \begin{aligned} BSIc = ToD^2 \space (mg/cm^3/1000) \cdot ToA.tb^2 \space (mm^2) \space \\[10pt] ToD: total \space density \\ ToA.tb: total \space area \end{aligned} \] Contour mode 1, peel mode 2 with a threshold of 710 mg/cm3 defined cortical bone measures at the 66% site. Cortical bone measures included bone mineral density (cBMD (mg/cm3)), a material property. Bone size was measured using cortical area (CoA ( mm2)) and bone architecture using total area (ToA (mm2)) and polar moment of inertia (MoI (mm4)). A composite strength measurement, SSIp (mm3) (see formula below; Cointry et al., 2014), that combined the material property (cBMD) with the architecture measure, MoI, polar strength-strain index. To determine the polar Strength-Strain Index (SSIp) a contour mode of 1, peel mode 2 and a threshold of 480 mm/cm3 was used.
\[ \begin{aligned} SSIp = (\frac{MoI}{D_{max}}) \cdot (\frac{CD}{ND}) \space \\[10pt] MoI: Moment \space of \space Inertia \\ D_{max} = maximum \space distance \space of \space a \space voxel \space from \space center \space of \space gravity \\ CD = measured \space cortical \space density \space (mg/cm^3) \space mineral \space per \space unit \space of \space cortical \space bone \space volume \\ ND = normal \space physiological \space density \space (1200 \space mg/cm^3) \end{aligned} \]
All scans were acquired and analyzed by 1 of 2 technicians holding Limited Permit X-Ray Technician certifications from the California Department of Public Health. The short-term in vivo precision (root-mean-square (RMS) -CV %) (Glüer et al., 1995) in our laboratory for tibial scans has been estimated between 0.5704% and 0.8957%. All scans were checked for movement artifacts at the time of the initial scan by the technician. Manufacturer supplied hydroxyapatite phantoms for pQCT were scanned daily prior to data collection.
Muscle Fitness Tests
Muscle fitness of the lower and upper limbs were assessed. Lower limb muscle fitness was assessed using a maximal vertical jump test and peak power at take-off was calculated (Sayers, Harackiewicz, Harman, Frykman, & Rosenstein, 1999). Upper limb fitness was measured using a bilateral hand grip test; absolute and relative measurements were collected.
Vertical Jump Test
Maximal jump height was measured using a Vertec™ (JUMPUSA.com, Sunnyvale, CA). Participants completed a warm-up and two practice jumps prior to testing. The participant’s standing reach was measured and three maximal countermovement vertical jumps (CMJ) were performed to displace the Vertec™ vanes with 20 seconds of rest between jumps. Maximal jump height was calculated as the difference between the jump height and the standing reach height. PP was calculated from the maximal jump height using the Sayer’s equation below (Sayers et al., 1999).
\[Peak \space Vertical \space Jump \space Power \space (W) = [51.9 * CMJ_{height} (cm)] + [48.9 * Body Mass (kg)] - 2007\]
Vertical Jump Reliability
Reliability of the above vertical jump height protocol was determined using 10 participants (Age 24.6 yr (3.0 yr); 5 female) who performed 3 maximal countermovement vertical jumps during 2 sessions that were 7 days apart. Maximal vertical jump height was then averaged for the 3 trials for each session and a Pearson correlation was run to determine reliability. The correlation coefficient for the test-retest of the vertical jump was r = 0.9902 95% CI (0.9577-0.9978).
Hand Grip Test
Maximal hand grip strength was measured for both hands using a handgrip dynamometer (BIOPAC System Inc., Goleta, CA) following a protocol based on the Canadian Physical Fitness and Lifestyle Approach (CPAFLA) (Canadian Society for Exercise Physiology, Canada, & Health Canada, 2003). Participants were instructed to stand in anatomical neutral with elbows extended and wrists in a neutral position. Participant’s dominant hand was determined by asking “Which hand do you write with?”. Starting with their dominant hand, participants completed three trials for each hand lasting 5 seconds with a 30 second recovery period. The highest peak to peak measurement for both dominant and nondominant hands were recorded and summed as combined grip strength (CGS). Relative grip strength (RGS) was calculated as CGS divided by body mass. Both RGS and CGS were used for analyses
Handgrip Reliability
Hand grip strength has been found to be a reliable measurement when standardized methods and calibrated dynamometers are used. Differences in assessors and brands of dynamometer minimally affect the high reliability (ICC > .9) and even time of day of the test did not significantly affect reliability results (Innes, 1999; Mathiowetz, Weber, Volland, & Kashman, 1984). In order to assess the stability of the measurement of one participant and within a group of participants the coefficient of variation (CV) was calculated. A CV of 10% for males and 12% for females was considered acceptable (Innes, 1999). The CV for CGS for 3 trials for each participant was calculated for a subset of our participants (n = 40; 20 from athlete population and 20 from control population). The average coefficient of variation (CV%) for the group was 6.35% (± 3.82%) and a median value of 5.14%.
Statistical Analyses
Statistical analyses were performed with SPSS 25.0 software (SPSS Inc, Chicago, Illinois). A one-way MANOVA was run to determine if athlete status affected the results; it did not (F (2,144) = 3.009, p = 0.052, Wilk’s λ = 0.960, partial η2 = 0.04)). As a result, the two datasets were merged for the final analyses. Preliminary analyses were performed to ensure there was not a violation of the assumption of normality for the predictor variables, RGS, CGS and PP, including tests for skewness and kurtosis, Kolmogorov-Smirnov test and assessment of the Q-Q plots. Outliers were assessed using the Mahalanobis distance statistic and no data were eliminated except for 8 participants who had no radial data and 3 participants who were missing data from the 4% radial site. The total number of participants used for each analysis are reported in the text and on the tables. Tests for linearity, multicollinearity and homoscedasticity were run. Correlation between RGS and PP was 0.346 indicating that multicollinearity was unlikely to be a problem (Tabachnick, Fidell, & Ullman, 2019). In addition, the variance inflation factors (VIF) was below 5 ranging from 1.578 - 1.606. Correlation between CGS and PP was 0.690 higher than RGS however the variance inflation factors (VIF) was below 5 ranging from 2.0 - 2.6 indicating that multicollinearity was unlikely to be a problem (Tabachnick, Fidell, & Ullman, 2019).
It was hypothesized that peak vertical jump power at take off (PP) calculated from a maximal vertical jump test explained a significant amount of variance of radial bone strength parameters compared to grip strength measurements (RGS and CGS). To test this hypothesis, hierarchical multiple regression (HMR; Bonferroni-adjusted p = 0.013; 0.05/4) was used to determine the amount of variance that the independent variables, RGS, CGS and PP, explained for bone strength parameters of the radius (cortical and trabecular regions) after controlling for the influence of sex. This statistical approach compared several regression models by adding RGS or CGS followed by PP to a model with sex (Model 1). Specifically, model 2 included sex and RGS/CGS and Model 3 included sex, RGS/CGS and PP. The dependent variables for the 66% radial diaphyseal bone site (cortical region) included SSIp, MoI, CoA and cBMD. The dependent variables for the 4% radial epiphyseal bone site (trabecular region) included vBMC.tb, vBMD.tb, ToA.tb and BSIc. Sex was entered in step 1 of the HMR as a control variable. Steps 2-3 involved entry order of the predictor variables, RGS/CGS (upper limb) and PP from vertical jump testing (lower limb). Post hoc power analyses were conducted for each HMR using the Free Statistics Calculator v 4.0. The sample size of 139 (female 78)/136 (female 75) was used for the statistical power analyses, the post hoc analyses indicated that statistical power for the cortical parameters (SSIp, MoI, CoA, and cBMD) and the trabecular parameters (vBMC.tb, vBMD.tb, ToA.tb, BSIc) HMR analyses ranged from 0.874-0.999 with cBMD at 0.052. Differences between the male and female participants were determined by unpaired t-tests (two-tailed) with a significance value of p < 0.05.
Results
Participants are described in Table 1. Males were significantly taller and larger, and had significantly greater muscle strength for all measures and greater bone strength at the radial 4% and 66% sites compared to females.
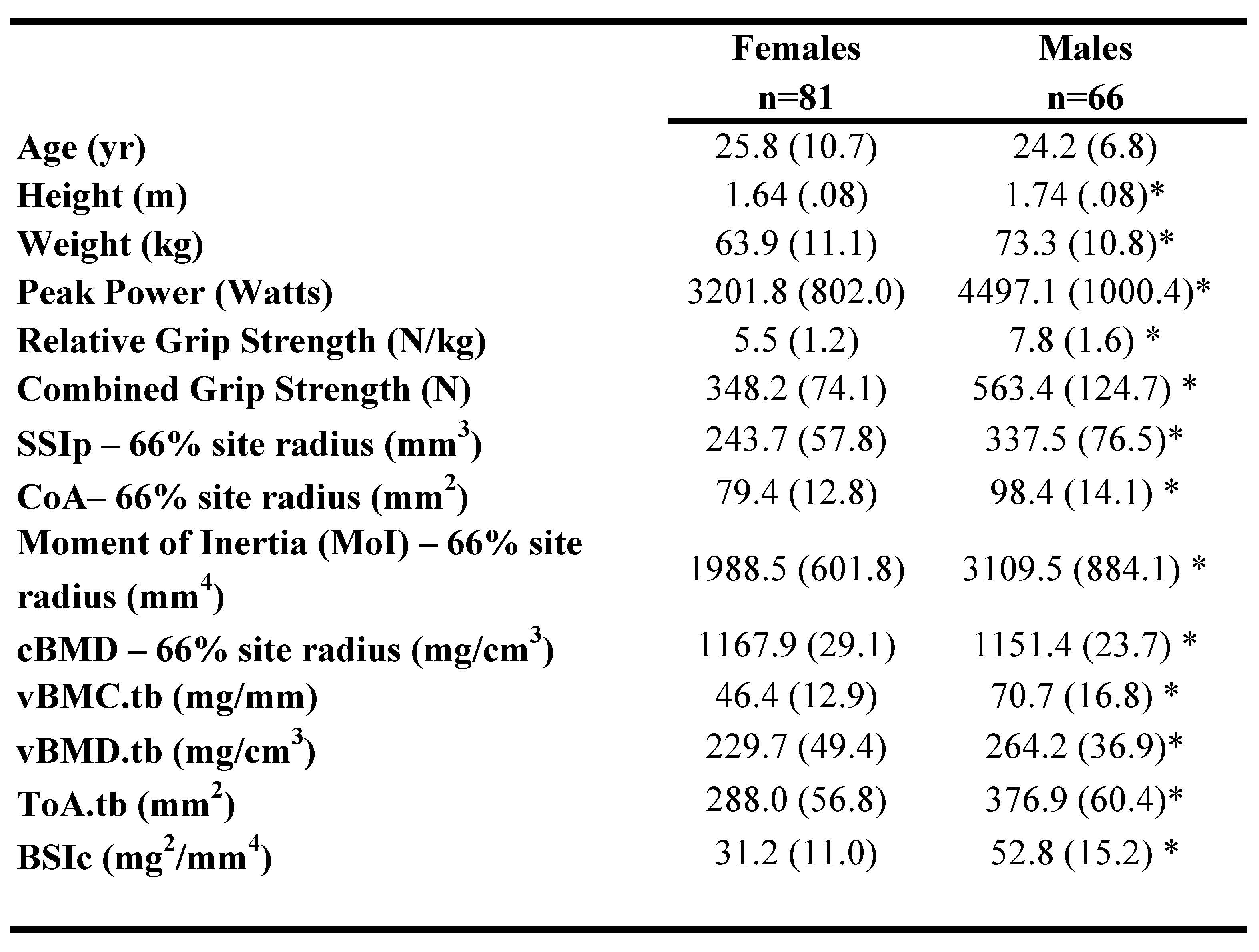
Table 1: Participant characteristics for Females and Males. Asterisk (*) indicates significant difference from Females.
The Pearson product-moment correlation coefficients indicated a positive association between the muscle fitness tests, RGS, CGS and peak vertical jump power (PP), and cortical bone strength measures at the 66% radial site: Cortical Area (CoA) (r = 0.505; p < 0.001; r = 0.744; p < 0.001; r = 0.731; p < 0.001 respectively), Moment of Inertia (MoI) (r = 0.518; p < 0.001; r = 0.741; p < 0.001; r = 0.697 ; p < 0.001 respectively) and polar Strength-Strain Index (SSIp) (r = 0.496; p < 0.001; r = 0.718; p < 0.001; r = 0.688 ; p < 0.001 respectively). However, RGS, CGS, and PP were inversely related to cBMD (r = -0.210; p = 0.007; r = -0.247; p = 0.002; r = -0.205; p=0.008 respectively).
The Pearson product-moment correlation coefficients indicated that RGS, CGS and PP were all significantly correlated with trabecular measures at the 4% radial site: Total Area (ToA.tb) (r = 0.408 ; p < 0.001; r = 0.609 ; p < 0.001; r = 0.567; p< 0.001 respectively), volumetric Bone Mineral Content (vBMC.tb) (r = 0.397 ; p < 0.001; r = 0.640; p < 0.001; r = 0.697; p < 0.001 respectively), volumetric Bone Mineral Density (vBMD.tb) (r = 0.192; p = 0.012; r = 0.362; p < 0.001; r = 0.529; p < 0.001 respectively) and Bone Strength Index-compression (BSIc) (r = 0.460; p < 0.001; r = 0.621; p < 0.001; r = 0.617; p < 0.001 respectively).
Trabecular Bone Site- 4% Radius
Four bone strength parameters were used as independent variables, vBMC.tb (mg/mm), vBMD.tb (mg/cm3), ToA.tb (mm2) and BSIc (mg/mm4). For all trabecular bone strength variables, sex explained between 12.7-40.3% of the variance (adjusted R2). For all outcome measures (vBMC.tb, vBMD.tb, ToA.tb, BSIc) of the trabecular region of the radius (4% scan site) model 2 (sex + RGS) was not significant, the change in adjusted R2 ranged from 0.1-0.8%. However, the addition of PP significantly increased adjusted R2 by 6.3% to 15.2% (Table 2). PP (Model 3 (ie. sex + RGS + PP)) explained the highest overall variance for vBMC.tb (54.8%) followed by BSIc (48.9%), ToA.tb (41.9%) and vBMD.tb with 26.7% (Table 2). PP had significantly higher standardized beta values compared to RGS for all variables (Table 2). A standardized beta coefficient compares the strength of the effect of each individual independent variable to the dependent variable. PP contributed 8.4% of unique variance for BSIc in Model 3 as indicated by the delta R2 values for a total of 48.9% explained variance and PP contributed more to the model than did sex and RGS (i.e., 0.366 vs. 0.337 and 0.129 standardized β-values) (Table 2). Model 3 explained 54.8% of the variance for vBMC.tb with PP contributing more to the model than did sex and RGS (i.e., 0.492 vs. 0.315 and 0.036 standardized β-values) (Table 2). Model 3 and in particular PP explained 41.9% of the total area of the trabecular region (ToA.tb). The standardized β-values for PP, sex and RGS were 0.317, 0.365 and 0.076 respectively. PP contributed more to the model for vBMD.tb than did sex and RGS (i.e., 0.488 vs. 0.083 and -0.027 standardized β-values) and explained 26.7% of the variance. Collectively, RGS was not a significant predictor of any bone strength parameter in the trabecular 4% site of the radius and PP was a significant predictor of bone strength in the trabecular region of the distal radius. Similar results were found using CGS in the model for vBMD.tb (Table 3). A significant change in R2 was found in Model 2 (sex + CGS) for vBMC.tb and BSIc (6.8% and 5.4% respectively) but when PP was added (Model 3 (ie. sex + CGS + PP)) only the standardized β-values for sex and PP were significant (Table 3). For T.Ar.tb, CGS remained a significant predictor variable in Model 3 along with sex and PP (i.e., 0.247, 0.295 and 0.217 standardized β-values respectively) (Table 3).
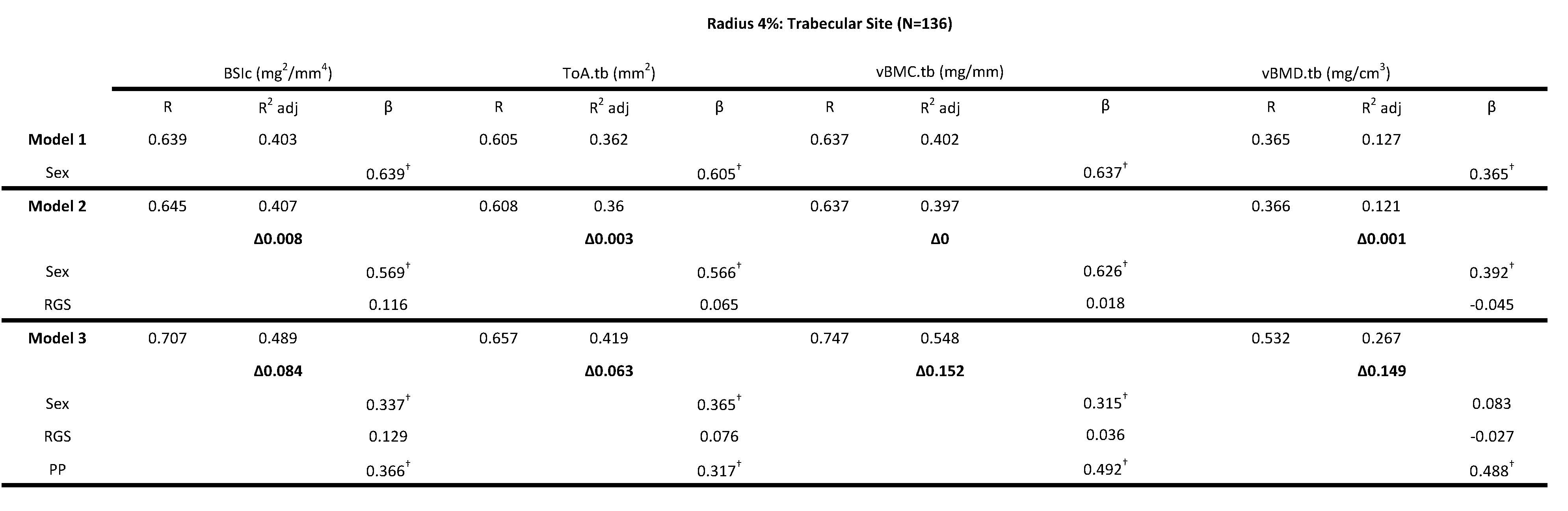
Table 2: Hierarchical multiple regression (HMR) analyses for predicting Bone Strength Index, BSIc (mg2/mm4), Total Area ToA.tb (mm2), Bone Mineral Content, vBMC.tb (mg/mm) and Bone Mineral Density vBMD.tb (mg/cm3) at the 4% radial site using sex, relative grip strength (RGS) and peak power (PP) as predictor variables. β is the Standardized beta coefficient indicates the predictive power. Adjusted coefficient of determination (R2 Adj) provides the amount of variation explained by the regression model. Δ indicates change in R2 from model 1 (bold). † Indicates a significant β
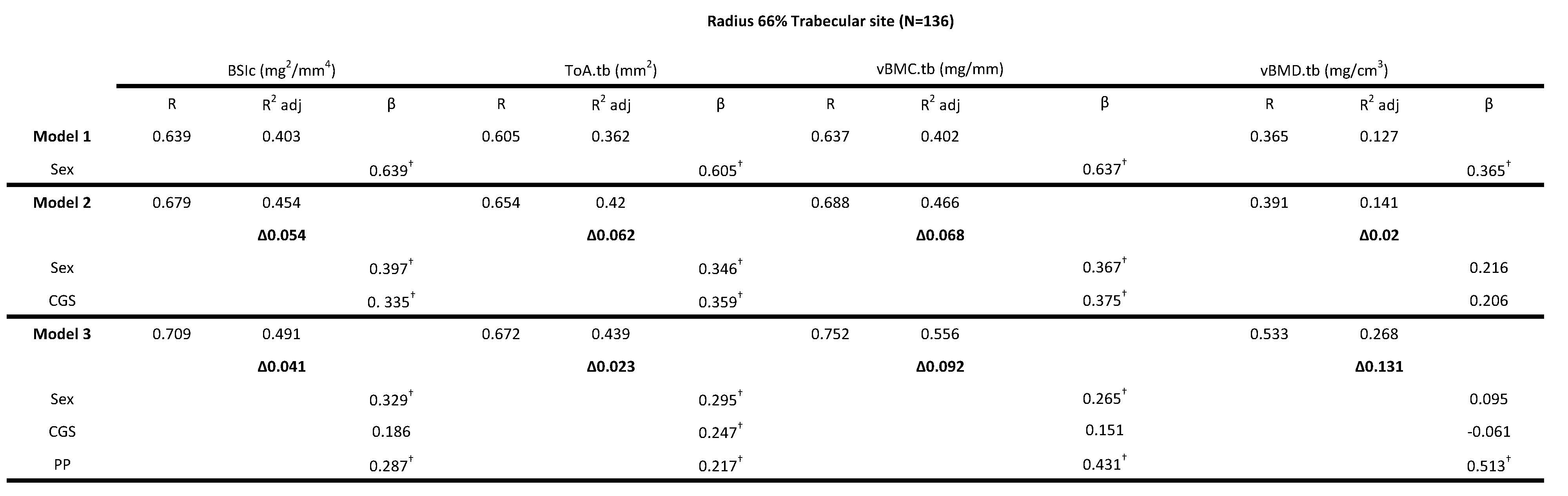
Table 3: Hierarchical multiple regression (HMR) analyses for predicting Bone Strength Index, BSIc (mg2/mm4), Total Area ToA.tb (mm2), Bone Mineral Content, vBMC.tb (mg/mm) and Bone Mineral Density vBMD.tb (mg/cm3) at the 4%radial site using sex, absolute combined grip strength (CGS) and peak power (PP) as predictor variables. β is the Standardized beta coefficient indicates the predictive power. Adjusted coefficient of determination (R2 Adj) provides the amount of variation explained by the regression model. Δ indicates change in R2 from model 1 (bold). † Indicates a significant β
Cortical Bone Site- 66% Radius
For the cortical bone site of the radius (66% site) RGS, CGS and PP significantly increased the explained variance (\(\Delta\)R2) for SSIp, MoI and CoA. However, PP explained 3-5x more of the variance in the bone strength variables compared to RGS but CGS explained 3-4x more that PP. Model 1 that only included Sex explained 32.6% of the total variance for SSIp (F(1,138) = 67.852, p <0.0001). The addition of RGS in Model 2 (ie. sex + RGS)) explained an additional 3.4% of the unique variance (FChange(1,136)=7.376, p<.0001), however, an additional 18.5% of the unique variance was explained by PP increasing the total explained variance of Model 3 (ie. sex + RGS + PP) to 54.1% (FChange(1,135)=55.638, p<.0001). Based on the standardized beta coefficients, PP (0.545, p<.0001) contributed more to the unique variance in bone strength parameters compared to RGS (0.250, p=.001). Similar results were found for MoI with RGS contributing 3.7% and PP 17.6% of total variance (56.8%) explained by Model 3 (ie. sex + RGS + PP) (F(3,138) = 61.438, p <0.0001) (Table 3). PP had a larger standardized beta coefficient (0.531, p<.0001) compared to RGS (0.257, p<.0001) and sex (0.123, p=.143). The overall model fit for Model 3 (ie. sex + RGS + PP) for cortical area was adjusted R2 = .597 (F (3,138) = 69.056, p <0.0001) with contributions of 3.8% from RGS and 23.2% from PP (Table 4). Again, PP had a higher beta coefficient (0.612, p<.0001) compared to RGS (0.236, p<.0001) and sex (0.044, p = 0.586). The addition of CGS to model 2 (ie. sex + RGS)) explained more of the unique variance compared to RGS, an additional 19-20% for CoA, MoI and SSIp (Table 5). An additional 5-8% of the unique variance was explained by PP increasing the total explained variance of Model 3 (ie. sex + RGS + PP) to 57.6-64.3%. Based on the standardized beta coefficients, PP was a significant contributor to the explained variance with CGS for CoA (i.e., 0.417 vs. 0.463 standardized β-values respectively), MoI (i.e., 0.338 vs. 0.461 standardized β-values respectively) and SSIp (i.e., 0.359 vs. 0.444 standardized β-values respectively) (Table 5). The models including RGS, CGS and PP did not explain a significant portion of the variance for cBMD, only sex was significant in the explained variance but to a very low level, the adjusted R2 for Model 3 (ie. sex + RGS + PP) was 6.9% (Tables 4). Collectively, HMR results indicate that RGS, CGS and PP were significant predictors of bone strength (SSIp, MoI, CoA), with PP contributing more unique variance compared to RGS and remaining a significant variable in the models with CGS.
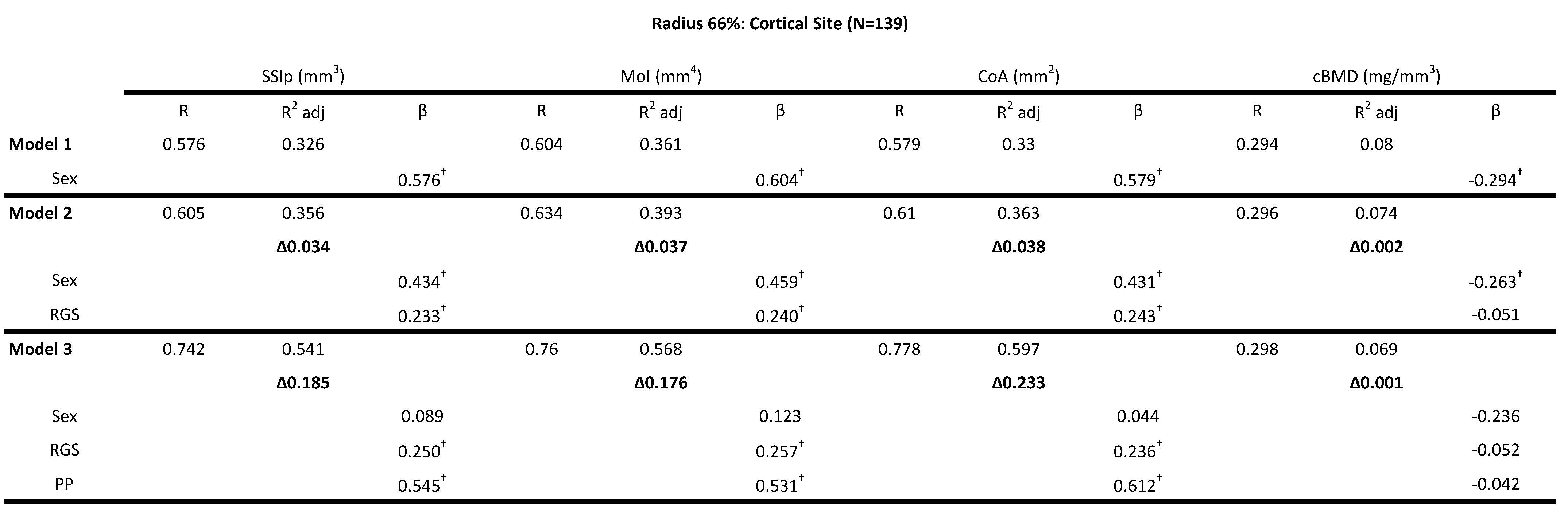
Table 4: Hierarchical multiple regression (HMR) analyses for predicting Bone Strength Index, SSIp (mm3)- Strength Strain Index, MoI (mm4)- polar Moment of inertia, CoA (mm2- Cortical Area, cBMD (mg/mm3)-Cortical Bone Mineral Density at the 66% radial site using sex, relative grip strength (RGS) and peak power (PP) as predictor variables. β is the Standardized beta coefficient indicates the predictive power. Adjusted coefficient of determination (R2 Adj) provides the amount of variation explained by the regression model. Δ indicates change in R2 from model 1 (bold). † Indicates a significant β
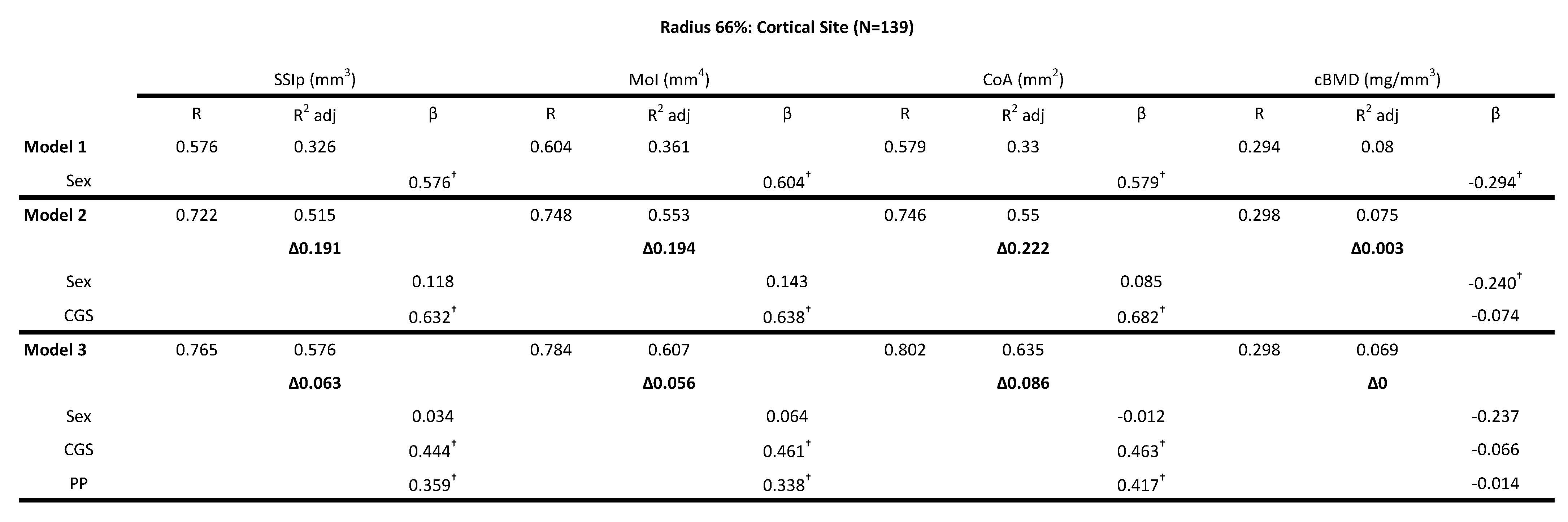
Table 5: Hierarchical multiple regression (HMR) analyses for predicting Bone Strength Index, SSIp (mm3)- Strength Strain Index, MoI (mm4)- polar Moment of inertia, CoA (mm2) - Cortical Area, cBMD (mg/mm3)-Cortical Bone Mineral Density at the 66% radial site using sex, absolute combined grip strength (CGS) and peak power (PP) as predictor variables. β is the Standardized beta coefficient indicates the predictive power. Adjusted coefficient of determination (R2 Adj) provides the amount of variation explained by the regression model. Δ indicates change in R2 from model 1 (bold). † Indicates a significant β
Discussion
Our results identified RGS and CGS to be significant predictors of radial strength parameters in the cortical region (66% site) but not in the trabecular region (4% site). Peak vertical jump power at take-off calculated from maximal vertical jump height was a stronger predictor of bone strength parameters of both cortical and trabecular compartments of the radius including polar SSIp, CoA and MoI and trabecular measures of vBMC.tb, vBMD.tb, ToA.tb and BSIc. The strong relationship between lower limb PP and bone strength parameters supports the use of the vertical jump as a surrogate for direct measures of bone health such as DXA and pQCT.
As expected, based on the literature (Kontulainen, Sievänen, Kannus, Pasanen, & Vuori, 2003), cBMD was not determined by PP, RGS or CGS in the current study. Bone mineral density is established early in development and is only one of many factors contributing to bone strength. Loading on bone via physical activity and sport results in greater bone strength via architectural changes rather than changes in material properties, cBMD, of the bone (Kontulainen et al., 2003). Trabecular density, vBMD.tb, has been found to increase along with trabecular measures of size and quantity of bone (ToA and vBMC.tb). However, trabecular density is not a true material property, and only indicates changes in the quantity of trabecular bone in that region.
Based on the current data, the lower limb muscle fitness test (vertical jump) was an equal or better indicator of radial bone strength compared to RGS or CGS. RGS was not associated with trabecular bone strength parameters in the radius but CGS was significant until PP was added to the analyses. However, there was a significant association between RGS, CGS and bone strength parameters in the cortical region of the radius (66% site). Yet, PP calculated from a maximal vertical jump was a stronger predictor of cortical bone strength parameters in a model with RGS and remained a significant determinant of bone strength in a model including CGS. The majority of studies on a wide age range of adults of both genders report significant correlations between grip strength and bone strength in cortical bone sites but weak correlations or non-significant findings were found for trabecular bone sites (Frank, Lorbergs, Chilibeck, Farthing, & Kontulainen, and Andrew William Frank, Labas, Johnston, & Kontulainen, 2012; Hasegawa, Schneider, & Reiners, 2001). When cortical bone was separated from trabecular bone at the 4% radial site, stronger correlations were reported for cortical bone areas (Boonen et al., 1997; Kaji et al., 2005). Wapniarz et al. (Wapniarz et al., 1997) found weak correlations with bone mineral content from the 4% radial site but that measurement included both cortical and trabecular bone. These previous studies only reported grip strength as the muscle function parameter or muscle cross-sectional area. The current data was a comparison of two muscle fitness tests and no significance was found between RGS and trabecular bone strength parameters and only weak associations with RGS in the cortical bone sites (66% site). Similarly, CGS was weakly associated with trabecular bone strength with increased strength of association in cortical bone sites while PP was also significant. It should be noted that one previous study on 18-year-old boys, assessing the second metacarpal cortical thickness and cortical area did not find a significant correlation with vertical jump height. However, these bone data were based on radiographs and thus structural parameters were determined from 2D cortical thickness (Dequeker & Van Tendeloo, 1982).
PP calculated from maximal vertical jump height has been reported to better predict bone strength in comparison to other muscle fitness tests, however, the majority of studies have focused on bones of the lower limb and not the upper limb. PP was significantly correlated to both SSIp (66% tibia site) and CoA (r = 0.69-0.78) in the tibia in 17-year-old males and females (Janz et al., 2015) and in collegiate athletes (Yingling et al., 2017). In older populations, power measured from a leg extension exercise was also found to be more predictive of tibial bone strength and geometry with significant relationships found between power and SSIp (r = 0.488) but not to muscle strength (r = 0.149) (Ashe, Liu-Ambrose, Cooper, Khan, & McKay, 2008). Baptista et al. (2016) reported a significant relationship between PP and BMD values at the femoral neck and radius (r = 0.75) in 8-year-old boys and girls (Baptista, Mil-Homens, Carita, Janz, & Sardinha, 2016). However, studies that focused on radial bone strength parameters predominantly used hand grip tests as a measure of muscle fitness since bone is thought to be site specific for adaptations to mechanical loading. The current results used both PP and hand grip strength to assess radial bone strength at both the trabecular and cortical regions and PP explained a significant percentage of both trabecular and cortical bone strength parameters. RGS and CGS were significant indicators of cortical bone strength parameters including CoA, SSIp and MoI, but PP explained 50% more of the variance compared to RGS at the cortical radial site and remained significant when compared to CGS. In fact, PP explained a significant percentage of trabecular bone strength parameters in the radius while RGS was not significantly related and CGS was weakly associated. The current data combined with previous studies indicate that PP measure may be better than RGS and CGS as a surrogate for bone strength parameters in both upper and lower limbs.
A major difference between grip strength and vertical jump testing is the impulsive nature of the jump compared to the isometric contraction of the grip strength test. During a vertical jump, the jumper applies an impulse to the ground to maximize the momentum and the vertical velocity in order to jump as high as possible. High impact loading, high intensity loading and variable loading patterns in activities such as basketball and volleyball require muscle power to a greater degree than maximal muscle strength. Muscle strength, defined as the capacity to generate force, differs from muscle power which is the product of force times velocity. Power is not just the ability to generate force but to generate force quickly, the velocity component differentiates muscle power from muscle strength. The rate and frequency of high velocity muscle contractions during power training apply higher loads and greater loading rates to tendons and bones. Loading rates and frequency are the factors that separate power training from strength training (Stengel, 2005). High loading rates and loading frequency are key osteogenic factors in bone along with magnitude and uniqueness of loading and the rest intervals between load sessions (Turner & Robling, 2003). Strain rates and load frequency are both anabolic and antiresorptive in bone (Hsieh, Robling, Ambrosius, Burr, & Turner, 2001; Mosley & Lanyon, 1998).
Impulsive activities may be better predictors of bone strength since they integrate both neuromuscular performance and body mass. Body mass is associated with bone strength as larger people have greater bone mass and strength. However, Rantalainen (2010) reported that although body mass was associated with bone size, neuromuscular factors add to significance in regression models at the tibia in both trabecular and cortical regions (Rantalainen et al., 2010). Impulse replaces body mass as a significant predictor in regression models for both BSI and SSI, impulse integrates both neuromuscular performance and body mass in a given physical performance (vertical jump). Maximal neuromuscular performance is a better indicator of bone loading environment than body mass.
Site specificity is a concept suggesting that bone responds to loading to the specific region loaded as opposed to systematic changes (Lanyon, 1996; Sugiyama, Price, & Lanyon, 2010). Most relevant are studies on racket sport athletes and recent data from baseball players in which the racket arm and throwing arm were found to have significantly greater moment of inertias (architectural adaptations) compared to control limb (Haapasalo et al., 2000; Warden, Bogenschutz, Smith, & Gutierrez, 2009). Based on these data it was hypothesized that a muscle strength measure of the upper limb (RGS and CGS) would better predict bone strength variance in the radius. However, the current data illustrated that PP calculated from a maximal vertical jump test was a better predictor of cortical and trabecular bone regions of the radius compared to a grip strength test. The integration of lower limb muscle fitness seems to have an impact on predicting bone strength. The velocity component of the impulse test may better reflect the overall skeletal health and be useful as a screening tool.
One strength of our study was that our participants were ethnically diverse, all ethnic groups and both genders were represented in the sample. Also, the use of pQCT analysis to measure bone strength indices and the use of multiple muscle fitness measures contributes to the strength of this study. One limitation of this study was that it was a cross-sectional design limiting the ability to examine cause and effect relationships. In addition, physical activity and nutrition are important factors to consider when investigating bone strength among a young adult population. These factors were not included in the current analyses since our purpose was not to determine factors that contribute to bone strength but to compare the associations between muscle function tests (hand grip strength and peak power) and bone strength traits to determine a surrogate measure for bone strength.
Conclusion
In summary, our investigation demonstrates peak power, calculated using maximal vertical jump height, explains a significant amount of variance of trabecular bone strength indices in the distal radius. In the cortical region, PP explains a greater amount of variance for bone strength indices than RGS, and PP explains a lesser but still significant amount of variance compared to CGS. Lower limb muscle power calculated from vertical jump height assessments may provide a simple, objective, valid and reliable measure to identify and monitor bone strength.
Additional Information
Data Accessibility
Data is available via a Dryad repository. Please cite data as: Yingling, Vanessa (2020), Data from: Peak vertical jump power predicts radial bone strength better than hand grip strength in healthy individuals, Dryad, Dataset, https://doi.org/10.5061/dryad.jh9w0vt7t
Conflict of Interest
Authors have no conflicts of interest to declare.
Funding
Support provided by the Cal State East Bay Center for Student Research Scholars Program (CSR).
Acknowledgments
We thank the Kinesiology Research Group (KRG) and the Cal State East Bay Athletic Department.
Preprint
The pre-publication version of this manuscript can be found on SportRxiv (DOI: 10.31236/osf.io/2t39k).
References
Ashe, M. C., Liu-Ambrose, T. Y. L., Cooper, D. M. L., Khan, K. M., & McKay, H. A. (2008). Muscle power is related to tibial bone strength in older women. Osteoporosis International, 19(12), 1725–1732. https://doi.org/10.1007/s00198-008-0655-6
Augat, P., Iida, H., Jiang, Y., Diao, E., & Genant, H. K. (1998). Distal radius fractures: mechanisms of injury and strength prediction by bone mineral assessment. Journal of Orthopaedic Research: Official Publication of the Orthopaedic Research Society, 16(5), 629–635. https://doi.org/10.1002/jor.1100160517
Baptista, F., Mil-Homens, P., Carita, A., Janz, K., & Sardinha, L. (2016). Peak vertical jump power as a marker of bone health in children. International Journal of Sports Medicine, 37(08), 653–658. https://doi.org/10.1055/s-0042-105290
Best, A., Holt, B., Troy, K., & Hamill, J. (2017). Trabecular bone in the calcaneus of runners. PLOS ONE, 12(11), e0188200. https://doi.org/10.1371/journal.pone.0188200
Boonen, S., Cheng, X. G., Nijs, J., Nicholson, P. H. F., Verbeke, G., Lesaffre, E., … Dequeker, J. (1997). Factors associated with cortical and trabecular bone loss as quantified by peripheral computed tomography (pQCT) at the ultradistal radius in aging women. Calcified Tissue International, 60(2), 164–170. https://doi.org/10.1007/s002239900208
Canadian Society for Exercise Physiology, Canada, & Health Canada. (2003). The Canadian physical activity, fitness & lifestyle approach: CSEP health & fitness program’s health-related appraisal & counselling strategy. Ottawa, Ont.: Canadian Society for Exercise Physiology.
Cointry, G., Ferretti, J. L., Reina, P. S., Nocciolono, L. M., Rittweger, J., & Capozza, R. F. (2014). The pQCT “Bone Strength Indices”(BSIs, SSI). Relative mechanical impact and diagnostic value of the indicators of bone tissue and design quality employed in their calculation in healthy men and pre-and post-menopausal women. Journal of Musculoskeletal and Neuronal Interactions, 14(1), 29–40.
Cooper, C., Campion, G., & Melton, L. J. (1992). Hip fractures in the elderly: A world-wide projection. Osteoporosis International: A Journal Established as Result of Cooperation between the European Foundation for Osteoporosis and the National Osteoporosis Foundation of the USA, 2(6), 285–289. https://doi.org/10.1007/bf01623184
Dequeker, J., & Van Tendeloo, G. (1982). Metacarpal bone mass and upper-extremity strength in 18-year-old boys. Investigative Radiology, 17(4), 427–429. https://doi.org/10.1097/00004424-198207000-00026
Ferretti, J. L., Cointry, G. R., Capozza, R. F., Capiglioni, R., & Chiappe, M. A. (2001). Analysis of biomechanical effects on bone and on the muscle-bone interactions in small animal models. Journal of Musculoskeletal & Neuronal Interactions, 1(3), 263–274.
Földhazy, Z., Arndt, A., Milgrom, C., Finestone, A., & Ekenman, I. (2005). Exercise-induced strain and strain rate in the distal radius. The Journal of Bone and Joint Surgery. British Volume, 87-B(2), 261–266. https://doi.org/10.1302/0301-620X.87B2.14857
Frank, A. W., Lorbergs, A. L., Chilibeck, P. D., Farthing, J. P., & Kontulainen, S. A. (2010). Muscle cross sectional area and grip torque contraction types are similarly related to pQCT derived bone strength indices in the radii of older healthy adults. Journal of musculoskeletal & neuronal interactions. 10. 136-41.
Frank, A. W., Labas, M. C., Johnston, J. D., & Kontulainen, S. A. (2012). Site-specific variance in radius and tibia bone strength as determined by muscle size and body mass. Physiotherapy Canada, 64(3), 292–301. https://doi.org/10.3138/ptc.2010-40BH
Glüer, C.-C., Blake, G., Lu, Y., Blunt, B. A., Jergas, M., & Genant, H. K. (1995). Accurate assessment of precision errors: how to measure the reproducibility of bone densitometry techniques. Osteoporosis International, 5(4), 262–270. https://doi.org/10.1007/BF01774016
Golden, N. H. (2000). Osteoporosis prevention: A pediatric challenge. Archives of Pediatrics & Adolescent Medicine, 154(6), 542–543.
Greene, D. A., Naughton, G. A., Bradshaw, E., Moresi, M., & Ducher, G. (2012). Mechanical loading with or without weight-bearing activity: Influence on bone strength index in elite female adolescent athletes engaged in water polo, gymnastics, and track-and-field. Journal of Bone and Mineral Metabolism, 30(5), 580–587. https://doi.org/10.1007/s00774-012-0360-6
Haapasalo, H., Kontulainen, S., Sievänen, H., Kannus, P., Järvinen, M., & Vuori, I. (2000). Exercise-induced bone gain is due to enlargement in bone size without a change in volumetric bone density: A peripheral quantitative computed tomography study of the upper arms of male tennis players. Bone, 27(3), 351–357. https://doi.org/10.1016/s8756-3282(00)00331-8
Hasegawa, Y., Schneider, P., & Reiners, C. (2001). Age, sex, and grip strength determine architectural bone parameters assessed by peripheral quantitative computed tomography (pQCT) at the human radius. Journal of Biomechanics, 34(4), 497–503. https://doi.org/10.1016/s0021-9290(00)00211-6
Hsieh, Y.-F., Robling, A. G., Ambrosius, W. T., Burr, D. B., & Turner, C. H. (2001). Mechanical loading of diaphyseal bone in vivo: The strain threshold for an osteogenic response varies with location. Journal of Bone and Mineral Research, 16(12), 2291–2297. https://doi.org/10.1359/jbmr.2001.16.12.2291
Innes, E. (1999). Handgrip strength testing: A review of the literature. Australian Occupational Therapy Journal, 46(3), 120–140. https://doi.org/10.1046/j.1440-1630.1999.00182.x
Janz, K. (2002). Physical activity and bone development during childhood and adolescence. Implications for the prevention of osteoporosis. Minerva Pediatrica, 54(2), 93–104.
Janz, K. F., Letuchy, E. M., Burns, T. L., Francis, S. L., & Levy, S. M. (2015). Muscle power predicts adolescent bone strength: Iowa Bone Development Study. Medicine & Science in Sports & Exercise, 47(10), 2201–2206. https://doi.org/10.1249/MSS.0000000000000648
Kaji, H., Kosaka, R., Yamauchi, M., Kuno, K., Chihara, K., & Sugimoto, T. (2005). Effects of age, grip strength and smoking on forearm volumetric bone mineral density and bone geometry by peripheral quantitative computed tomography: Comparisons between Female and Male. Endocrine Journal, 52(6), 659–666. https://doi.org/10.1507/endocrj.52.659
Kannus, P., Haapasalo, H., Sankelo, M., Sievänen, H., Pasanen, M., Heinonen, A., … Vuori, I. (1995). Effect of starting age of physical activity on bone mass in the dominant arm of tennis and squash players. Annals of Internal Medicine, 123(1), 27–31. https://doi.org/10.7326/0003-4819-123-1-199507010-00003
Kontulainen, S. A., Johnston, J. D., Liu, D., Leung, C., Oxland, T. R., & McKay, H. A. (2008). Strength indices from pQCT imaging predict up to 85% of variance in bone failure properties at tibial epiphysis and diaphysis. Journal of Musculoskeletal & Neuronal Interactions, 8(4), 401–409.
Kontulainen, S., Sievänen, H., Kannus, P., Pasanen, M., & Vuori, I. (2003). Effect of long-term impact-loading on mass, size, and estimated strength of humerus and radius of female racquet-sports players: A Peripheral quantitative computed tomography study between young and old starters and controls. Journal of Bone and Mineral Research, 18(2), 352–359. https://doi.org/10.1359/jbmr.2003.18.2.352
Lambert, C., Beck, B. R., Harding, A. T., Watson, S. L., & Weeks, B. K. (2019). Impact versus resistance training for bone in young women: Preliminary Findings Of The OPTIMA-Ex Trial: 3067 Board #113 May 31 3:30 PM - 5:00 PM. Medicine & Science in Sports & Exercise, 51(Supplement), 845. https://doi.org/10.1249/01.mss.0000563025.70640.3b
Lanyon, L. E. (1996). Using functional loading to influence bone mass and architecture: Objectives, mechanisms, and relationship with estrogen of the mechanically adaptive process in bone. Bone, 18(1 Suppl), 37S-43S. https://doi.org/10.1016/8756-3282(95)00378-9
Lorbergs, A. L., Farthing, J. P., Baxter-Jones, A. D. G., & Kontulainen, S. A. (2011). Forearm muscle size, strength, force, and power in relation to pQCT-derived bone strength at the radius in adults. Applied Physiology, Nutrition, and Metabolism = Physiologie Appliquée, Nutrition Et Métabolisme, 36(5), 618–625. https://doi.org/10.1139/h11-065
Macdonald, H., Kontulainen, S., Petit, M., Janssen, P., & McKay, H. (2006). Bone strength and its determinants in pre- and early pubertal boys and girls. Bone, 39(3), 598–608. https://doi.org/10.1016/j.bone.2006.02.057
Marks, R. (2009). Hip fracture epidemiological trends, outcomes, and risk factors, 1970–2009. International Journal of General Medicine, 1. https://doi.org/10.2147/IJGM.S5906
Mathiowetz, V., Weber, K., Volland, G., & Kashman, N. (1984). Reliability and validity of grip and pinch strength evaluations. The Journal of Hand Surgery, 9(2), 222–226. https://doi.org/10.1016/s0363-5023(84)80146-x
Mosley, J. R., & Lanyon, L. E. (1998). Strain rate as a controlling influence on adaptive modeling in response to dynamic loading of the ulna in growing male rats. Bone, 23(4), 313–318. https://doi.org/10.1016/s8756-3282(98)00113-6
Nellans, K. W., Kowalski, E., & Chung, K. C. (2012). The epidemiology of distal radius fractures. Hand Clinics, 28(2), 113–125. https://doi.org/10.1016/j.hcl.2012.02.001
Rantalainen, T., Nikander, R., Heinonen, A., Multanen, J., Häkkinen, A., Jämsä, T., … Sievänen, H. (2010). Neuromuscular performance and body mass as indices of bone loading in premenopausal and postmenopausal women. Bone, 46(4), 964–969. https://doi.org/10.1016/j.bone.2010.01.002
Sayers, S. P., Harackiewicz, D. V., Harman, E. A., Frykman, P. N., & Rosenstein, M. T. (1999). Cross-validation of three jump power equations. Medicine and Science in Sports and Exercise, 31(4), 572–577. https://doi.org/10.1097/00005768-199904000-00013
Schoenau, E., Neu, C. M., Beck, B., Manz, F., & Rauch, F. (2002). Bone mineral content per muscle cross-sectional area as an index of the functional muscle-bone unit. Journal of Bone and Mineral Research: American Society for Bone and Mineral Research, 17(6), 1095–1101. https://doi.org/10.1359/jbmr.2002.17.6.1095
Stengel, S. V. (2005). Power training is more effective than strength training for maintaining bone mineral density in postmenopausal women. Journal of Applied Physiology, 99(1), 181–188. https://doi.org/10.1152/japplphysiol.01260.2004
Sugiyama, T., Price, J. S., & Lanyon, L. E. (2010). Functional adaptation to mechanical loading in both cortical and cancellous bone is controlled locally and is confined to the loaded bones. Bone, 46(2), 314–321. https://doi.org/10.1016/j.bone.2009.08.054
Sumnik, Z., Land, C., Coburger, S., Neu, C., Manz, F., Hrach, K., & Schoenau, E. (2006). The muscle-bone unit in adulthood: Influence of sex, height, age and gynecological history on the bone mineral content and muscle cross-sectional area. Journal of Musculoskeletal and Neuronal Interactions, 6(2), 195.
Turner, C. H., & Robling, A. G. (2003). Designing exercise regimens to increase bone strength. Exercise and Sport Sciences Reviews, 31(1), 45–50. https://doi.org/10.1097/00003677-200301000-00009
Van der Meulen, M. C. H., Jepsen, K. J., & Mikić, B. (2001). Understanding bone strength: Size isn’t everything. Bone, 29(2), 101–104.https://doi.org/10.1016/s8756-3282(01)00491-4
Wapniarz, M., Lehmann, R., Reincke, M., Schönau, E., Klein, K., & Allolio, B. (1997). Determinants of radial bone density as measured by PQCT in pre- and postmenopausal women: The role of bone size. Journal of Bone and Mineral Research, 12(2), 248–254. https://doi.org/10.1359/jbmr.1997.12.2.248
Warden, S. J., Mantila Roosa, S. M., Kersh, M. E., Hurd, A. L., Fleisig, G. S., Pandy, M. G., & Fuchs, R. K. (2014). Physical activity when young provides lifelong benefits to cortical bone size and strength in men. Proceedings of the National Academy of Sciences, 111(14), 5337–5342. https://doi.org/10.1073/pnas.1321605111
Warden, Stuart J., Bogenschutz, E. D., Smith, H. D., & Gutierrez, A. R. (2009). Throwing induces substantial torsional adaptation within the midshaft humerus of male baseball players. Bone, 45(5), 931–941. https://doi.org/10.1016/j.bone.2009.07.075
Warden, Stuart J., Carballido-Gamio, J., Avin, K. G., Kersh, M. E., Fuchs, R. K., Krug, R., & Bice, R. J. (2019). Adaptation of the proximal humerus to physical activity: A within-subject controlled study in baseball players. Bone, 121, 107–115. https://doi.org/10.1016/j.bone.2019.01.008
Yingling, V. R., Webb, S. L., Inouye, C., O, J., & Sherwood, J. J. (2020). Muscle Power Predicts Bone Strength in Division II Athletes. Journal of strength and conditioning research, 34(6), 1657–1665. https://doi.org/10.1519/JSC.0000000000002222
Communications in Kinesiology